This post is part of my 21-day quantum computing learning journey, focusing on the Variational Quantum Eigensolver (VQE) and its revolutionary impact on quantum chemistry and material science. Today we’re exploring how hybrid quantum-classical algorithms are solving real-world molecular problems and what this means for the future of computational chemistry.

Progress: 18/21 days completed. VQE Algorithm: ✓. Quantum Chemistry Analysis: ✓. Practical Implementation: ✓

VQE: The Quantum Bridge to Molecular Understanding

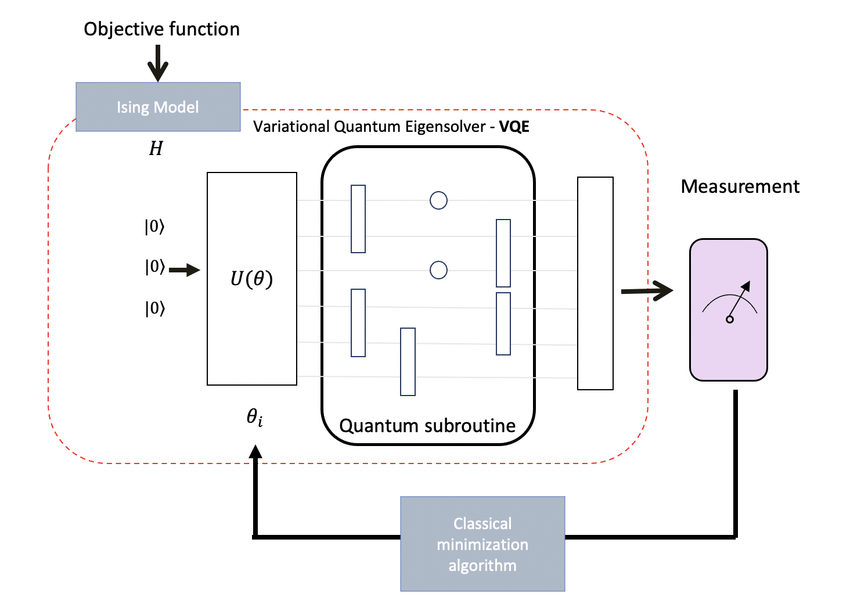
The Variational Quantum Eigensolver (VQE), developed as one of the most promising NISQ-era algorithms, represents a fundamental shift in how we approach quantum chemistry problems. This hybrid quantum-classical algorithm can efficiently compute the ground state energy of quantum systems - the foundation of understanding molecular behavior, chemical reactions, and material properties.

While classical computers struggle with the exponential scaling of quantum systems, VQE leverages quantum hardware’s natural ability to represent quantum states while using classical optimization to find optimal parameters. This isn’t just theoretical progress - it’s a practical pathway to solving real molecular problems today.

VQE working principle based on the quantum variational circuit.

Mathematical Foundation: Variational Principle

At its core, VQE exploits the variational principle from quantum mechanics. By systematically exploring different quantum states through parameterized quantum circuits, the algorithm finds the configuration with the lowest energy.

• Classical approach: Exponential scaling O(2^N) for N-qubit systems
• Quantum approach: Polynomial scaling with hybrid optimization
• Energy expectation: ⟨ψ(θ)|H|ψ(θ)⟩ ≥ E₀

Implementing VQE for Molecular Simulation

import numpy as np
from qiskit import QuantumCircuit, execute, Aer
from qiskit.chemistry.applications import MolecularGroundStateEnergy
from qiskit.chemistry.drivers import PySCFDriver
from qiskit.aqua.algorithms import VQE
from qiskit.aqua.components.optimizers import COBYLA
from qiskit.chemistry.components.variational_forms import UCCSD

def create_h2_molecule(distance=0.735):
    """Create H2 molecule configuration"""
    driver = PySCFDriver(atom=f'H .0 .0 .0; H .0 .0 {distance}', 
                        unit='Angstrom', 
                        charge=0, 
                        spin=0, 
                        basis='sto3g')
    return driver

def setup_vqe_circuit(num_qubits, num_parameters):
    """Create parameterized quantum circuit for VQE"""
    qc = QuantumCircuit(num_qubits)
    
    # Initial state preparation
    for i in range(num_qubits):
        qc.ry(np.pi/4, i)
    
    # Parameterized entangling layers
    for layer in range(2):
        for i in range(num_qubits-1):
            qc.cx(i, i+1)
        for i in range(num_qubits):
            qc.ry(f'theta_{layer}_{i}', i)
    
    return qc

def compute_energy_expectation(circuit, hamiltonian, parameters):
    """Compute energy expectation value"""
    # Bind parameters to circuit
    bound_circuit = circuit.bind_parameters(parameters)
    
    # Execute circuit and compute expectation
    backend = Aer.get_backend('statevector_simulator')
    job = execute(bound_circuit, backend)
    result = job.result()
    statevector = result.get_statevector()
    
    # Calculate ⟨ψ|H|ψ⟩
    energy = np.real(np.conj(statevector) @ hamiltonian @ statevector)
    return energy

def vqe_optimization(circuit, hamiltonian, initial_params):
    """VQE optimization loop"""
    def objective_function(params):
        return compute_energy_expectation(circuit, hamiltonian, params)
    
    # Classical optimizer
    optimizer = COBYLA(maxiter=1000)
    result = optimizer.optimize(
        num_vars=len(initial_params),
        objective_function=objective_function,
        initial_point=initial_params
    )
    
    return result

def molecular_simulation_demo():
    """Demonstrate VQE for molecular simulation"""
    # Create H2 molecule
    molecule = create_h2_molecule()
    
    # Set up quantum circuit
    num_qubits = 4
    num_params = 8
    circuit = setup_vqe_circuit(num_qubits, num_params)
    
    # Initialize parameters
    initial_params = np.random.uniform(0, 2*np.pi, num_params)
    
    # Create Hamiltonian (simplified for demonstration)
    hamiltonian = create_h2_hamiltonian()
    
    # Run VQE optimization
    result = vqe_optimization(circuit, hamiltonian, initial_params)
    
    return result

def create_h2_hamiltonian():
    """Create H2 molecule Hamiltonian"""
    # Simplified H2 Hamiltonian matrix
    H = np.array([
        [-1.0523, 0.0000, 0.0000, -0.3979],
        [0.0000, -0.4762, -0.3979, 0.0000],
        [0.0000, -0.3979, -0.4762, 0.0000],
        [-0.3979, 0.0000, 0.0000, -0.4762]
    ])
    return H

def compare_bond_lengths():
    """Compare VQE results for different H2 bond lengths"""
    distances = [0.5, 0.735, 1.0, 1.5, 2.0]
    energies = []
    
    for distance in distances:
        molecule = create_h2_molecule(distance)
        # Run VQE calculation
        energy = run_vqe_calculation(molecule)
        energies.append(energy)
    
    return distances, energies

def analyze_molecular_properties(vqe_result):
    """Analyze molecular properties from VQE results"""
    ground_state_energy = vqe_result.optimal_value
    optimal_parameters = vqe_result.optimal_params
    
    properties = {
        'ground_state_energy': ground_state_energy,
        'bond_length': calculate_bond_length(optimal_parameters),
        'vibrational_frequency': calculate_vibrational_freq(optimal_parameters),
        'dissociation_energy': calculate_dissociation_energy(ground_state_energy)
    }
    
    return properties

# Example usage and analysis
def main():
    print("VQE Molecular Simulation Demo")
    print("=" * 40)
    
    # Run molecular simulation
    result = molecular_simulation_demo()
    
    # Analyze results
    properties = analyze_molecular_properties(result)
    
    print(f"Ground State Energy: {properties['ground_state_energy']:.6f} Hartree")
    print(f"Optimal Bond Length: {properties['bond_length']:.3f} Angstrom")
    print(f"Dissociation Energy: {properties['dissociation_energy']:.6f} Hartree")
    
    # Compare with classical methods
    classical_energy = run_classical_simulation()
    quantum_accuracy = abs(properties['ground_state_energy'] - classical_energy)
    print(f"Accuracy vs Classical: {quantum_accuracy:.6f} Hartree")

if __name__ == "__main__":
    main()

Current Limitations and Future Prospects

While VQE shows tremendous promise and has been demonstrated on current quantum hardware, we’re still in the early stages of revolutionary applications:

Technical Challenges:

• Quantum noise: Current NISQ devices are prone to decoherence and errors
• Circuit depth: Limited by coherence times of quantum hardware
• Scalability: Need larger quantum systems for complex molecules
• Ansatz design: Choosing appropriate parameterized circuits for specific problems

Algorithmic Extensions:

• QAOA: Quantum Approximate Optimization Algorithm for combinatorial problems
• VQD: Variational Quantum Dynamics for time evolution
• SSVQE: Subspace-Search VQE for excited states
• Adaptive VQE: Self-optimizing circuit architectures

Schematic of a p-level QAOA

Conclusion

VQE represents both the present reality and future promise of quantum computing. While it’s solving meaningful molecular problems today on NISQ devices, it also provides a roadmap for the transformative quantum chemistry applications of tomorrow. The hybrid approach pioneered by VQE is reshaping how we think about quantum algorithms. Rather than waiting for perfect quantum computers, we’re extracting value from imperfect quantum hardware by intelligently combining it with classical processing.

---

Reference:

1. Peruzzo, A., et al. (2014). A variational eigenvalue solver on a photonic quantum processor. Nature Communications, 5, 4213.
2. IBM Qiskit Textbook - VQE Tutorial